Batch 3 - Class 147 - Game of "Mate"
Preclass Exercise:
- Five school girls were weighed in pairs and found to be 129, 125, 124, 123, 122, 121, 120, 118, 116 and 114 pounds. How much do they weight individually?
- Answer: 56, 58, 60, 64, 65. Reasoning below
- All girls must weight different, otherwise there would be repetition in pair weights. Let weights be a>b>c>d>e. Then largest weight must be a+b, then a+c. Lightest must be e+d, and then e+c. Sum of all the pair wise weights is 4(a+b+c+d+e) = 1212, and hence (a+b+c+d+e) = 303. Now c = (a+b+c+d+e)- (a+b) - (d+e) = 1212 - 129 - 114 = 60. a+c = 125, and hence a = 65, and a+b = 129, so b = 64. Similarly the rest.
Attendance: Smiti, Muskaan, Anshi, Siddhant, Arnav, Anishka, Liza, Arjun, Zorawar, Damini
Class Notes:
Game of Mate by G. Capellen
This is a two player game. From a standard deck of cards, pick A, 10, K, Q, 7 of each suit, with that rank order, and clubs > spade > heart > diamond. First player X deals ten cards each. The dealer leads a card, and the opponent, Y, plays next. If Y has a card of the same suit, she must play that. If she doesn't, she must play the same rank (another suit). If she doesn't have that either, its a MATE! Each move is won by the player as per rank of the card (if the same suit is played), or suit (if the same suit is not available and the same rank is played). The person who wins each move leads next. If all ten moves can be played without a mate, the game ends in a draw. The cards, as they are played, are kept face up in front of the player, and are not discarded.
The person who mates gets points equal to rank value (A=11, 10=10, K=4, Q=3, 7=7) multiplied by the move number in which mate happened. For example if a player gives a mate with a queen in the fourth move, she scores 3x4=12 points. Once a hand is finished, next hand is played with same set of cards exchanged between the two players, so that any element of luck is taken out. These two games constitute a round.
Let kids play 2 rounds of the game with different players, and then discuss strategies for winning the game.
Homework:
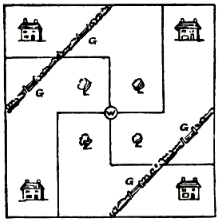
(536Henry: Problem 297) Here is a square plot of land with four houses, four trees, a well (W) in the center, and hedges planted across the four gateways (G). Can you divide the ground so that each householder shall have an equal portion of land, one tree, one gateway, an equal length of hedge, and free access to the well without trespass?
.png)
- Answer:
References:
536 Puzzles and Curious Problems, Henry Dudeney
A Gamut of Games, Sid Sackson